Rumus ABC: Pengertian, Soal dan Pembahasan

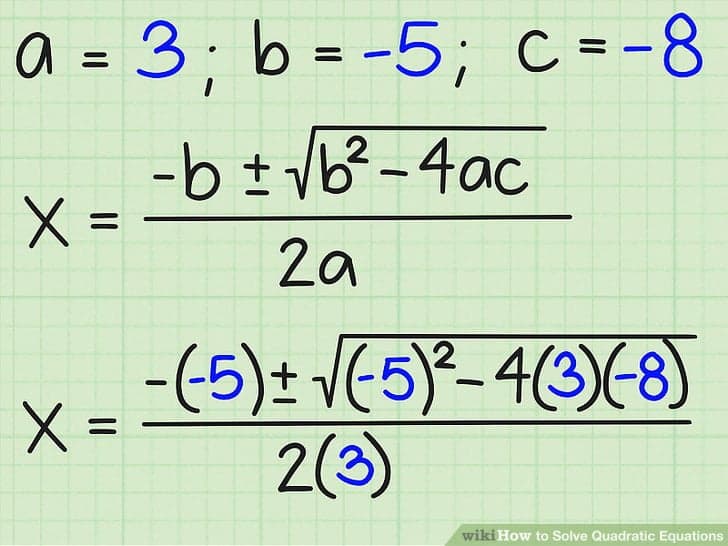
Rumus ABC merupakan cara yang unggul karena dapat digunakan untuk menemukan akar-akar dari berbagai bentuk persamaan kuadrat walaupun hasilnya tidak sebagai bilangan bulat.

Persamaan kuadrat ax² + bx + c = 0 dapat diselesaikan menggunakan beberapa metode. Diantaranya adalah metode pemfaktoran, melengkapi kuadrat dan rumus ABC.

Diantara beberapa cara tersebut, rumus abc merupakan cara yang unggul karena dapat digunakan untuk menemukan akar-akar dari berbagai bentuk persamaan kuadrat walaupun hasilnya tidak sebagai bilangan bulat.

Berikut penjelasan lanjut mengenai rumus tersebut, meliputi pengertian, soal, dan pembahasan.

Pengertian Rumus ABC

Rumus abc adalah salah satu rumus yang digunakan digunakan untuk mencari akar-akar persamaan kuadrat. Berikut merupakan bentuk umum dari rumus ini.

Huruf-huruf a, b, dan c dalam rumus abc disebut sebagai koefisien. Koefisien kuadrat x² adalah a, koefisien x adalah b, dan c adalah koefisien konstan, biasanya disebut sebagai konstanta atau suku bebas.

Persamaan kuadrat pada dasarnya merupakan persamaan matematika yang membentuk geometri lengkung parabola dalam kuadran xy.

Nilai koefisien dalam rumus abc mempunyai beberapa arti sebagai berikut:

• a menentukan cekung/cembungnya prabola yang dibentuk oleh persamaan kuadrat. Jika nilai a>0 maka parabola akan terbuka ke atas. Namun, jika a<0 maka parabola akan terbuka ke bawah.
• b menentukan posisi x puncak parabol, atau usmbu simetri cermin dari kurva yang dibentuk. Posisi tepat sumbu simetri adalah -b/2a dari persamaan kuadrat.
• c menentukan titik potong fungsi persamaan kuadrat parabola yang dibentuk dengan sumbu y atau saat nilai x=0.

Contoh Soal dan Pembahasan

Berikut beberapa contoh soal persamaan kuadrat beserta pembahasannya dengan penyelesaian menggunakan rumus persamaan kuadrat.

1. Selesaikan akar – akar dari persamaan kuadrat x² + 7x + 10 = 0 dengan menggunakan rumus abc!

Jawab :

diketahui a=1, b=7, dan c=10

maka, akar-akar persamaan tersebut adalah:

Jadi, hasil akar-akar dari persamaan x² + 7x + 10 = 0 adalah x = -2 atau x = -5

2. Dengan menggunakan rumus abc, tentukan himpunan penyelesaian dari x² + 2x = 0

Jawab :

diketaui a = 1 , b = 1, c = 0

maka akar-akar dari persamaan tersebut adalah sebagai berikut:

Jadi, hasil akar-akar dari persamaan x² + 2x = 0 adalah x1= 0 dan x2= -2, sehingga himpunan penyelesaiannya adalah HP = { -2,0 }

3. Carilah himpunan akar x pada soal x² – 2x – 3 = 0 dengan rumus abc

Jawab :

diketahui a = 1, b = 2, c = -3

maka hasil akar-akar dari persamaan tersebut adalah sebagai berikut:

Jadi, dengan x1= -1 dan x2=-3, himpunan penyelesaiannya adalah HP = { -1,3 }

4. Tentukan hasil persamaan kuadrat x² + 12x + 32 = 0 dengan menggunakan rumus abc !

Jawab :

diketahui a = 1, b=12, dan c =32

maka akar-akar persamaan tersebut adalah sebagai berikut:

Jadi, hasil akar-akar persamaan kuadrat nya adalah -4 dan -8

5. Tentukan himpunan dari soal berikut ini 3x² – x – 2 = 0

Jawab :

diketahui a = 3, b = -1, c = -2

maka akar-akar persamaan tersebut adalah sebagai berikut:

Jadi, akar-akar persamaan kuadrat 3x² – x – 2 = 0 adalah x1=1, dan x2=-2/3, sehingga himpunan penyelesaiannya adalah HP = { 1,-2/3 }

6. Tentukan akar-akar dari persamaan x² + 8x + 12 = 0 dengan menggunakan rumus abc!

Jawab:

diketahui a=1, b=8, dan c=12

maka akar-akar persamaan kuadrat adalah sebagai berikut:

Jadi, akar-akar persamaan kuadrat x² + 8x + 12 = 0 adalah x1 = -6 atau x2 = -2 sehingga himpunan penyelesaiannya adalah HP = { -6, -2}

7. Selesaikan akar-akar persamaan x² – 6x – 7 = 0 dengan rumus abc.

Jawab:

diketahui a=1, b= – 6 , dan c= – 7

maka akar-akar dari persamaan tersebut adalah sebagai berikut:

Jadi akar-akarnya adalah x₁ = 1 atau x₂ = 5/2 sehingga himpunan penyelesaiannya adalah HP = {1, 5/2 }.

8. Tentukan akar dari persamaan 2x² – 7x + 5 = 0 dengan rumus abc

Jawab:

diketahui a = 2, b = – 7 , dan c = 5

maka akar-akar dari persamaan tersebut adalah sebagai berikut:

Jadi akar-akarnya adalah x1 = –4 atau x2 = 5/3 sehingga himpunan penyelesaiannya adalah HP = {1, 5/3 }.

9. Selesaikan persamaan 3x² + 7x – 20 = 0 dengan rumus abc.

Jawab:

diketahui a = 3, b = 7, dan c = – 20

maka akar- akar dari persamaan tersebut adalah:

Jadi akar-akarnya adalah x1 = –4 atau x2 = 5/3 sehingga himpunan penyelesaiannya adalah HP = {-4, 5/3 }.

10. Tentukan akar-akar dari persamaan 2x² + 3x +5 = 0 dengan rumus abc.

Jawab:

diketahui a = 2, b = 3, dan c = 5

maka akar-akar dari persamaan tersebut adalah sebagai berikut:

Hasil dari akar persamaan 2x² + 3x +5 = 0 mempunyai bilangan akar imajiner √–31, sehingga persamaan tersebut tidak mempunyai penyelesaian. Himpunan penyelesaiannya ditulis sebagai himpunan kosong HP = { ∅ }

Demikian penjelasan mengenai pengertian rumus abc dengan contoh soal dan pembahasannya. Semoga bermanfaat!